Kurtosis function

---

The “peakedness” or flatness of the graph of a frequency distribution especially with respect to the concentration of values near the mean as compared with the normal distribution.

Measure of the relative concentration (flatness or peakedness) of data values in the center versus in the tails of a frequency distribution when compared with normal distribution (which has a kurtosis of 3). Distributions having higher kurtosis have fatter tails or more extreme values (a phenomenon called 'leptokurtosis'), and those with lower kurtosis have fatter middles or fewer extreme value (a phenomenon called 'platykurtosis'). From the Greek 'kyrtosis,' convexity.

Kurtosis (the term first used by Pearson, 1905) measures the "peakedness" of a distribution. If the kurtosis is clearly different than 0, then the distribution is either flatter or more peaked than normal; the kurtosis of the normal distribution is 0.

Calculation:

Kurtosis = [n*(n+1)*M4 - 3*M2*M2*(n-1)]/[(n-1)*(n-2)*(n-3)*4]

where:
Mj     is equal to: (xi-Meanx)j
 n       is the valid number of cases
4     is the standard deviation (sigma) raised to the fourth power

Skewness and kurtosis

Skewness and kurtosis describe the shape of your data set's distribution.  Skewness indicates how symmetrical the data set is, while kurtosis indicates how heavy your data set is about its mean compared to its tails.  Perfectly symmetrical data sets will have a skewness of zero, and a normally distributed data set will have a kurtosis of approximately three.

For example, this histogram (with an overlay of what a perfect normal distribution would have been) represents the total sample set available in the Access database included with this article:

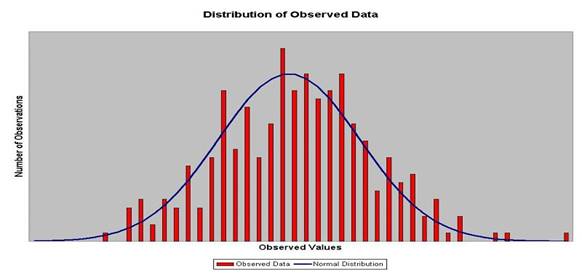
As we can see, the sample set is reasonably symmetrical, and the overall distribution appears to be close to a normal distribution, and thus we would expect to find a skewness of close to zero, and a kurtosis of close to three.

(Note: While a normal distribution has kurtosis ˜ 3, other distributions can have a kurtosis of 3, and thus you cannot use kurtosis alone to test the likelihood that your sample was drawn from a normal distribution.  Statisticians have devised numerous other normality tests.)

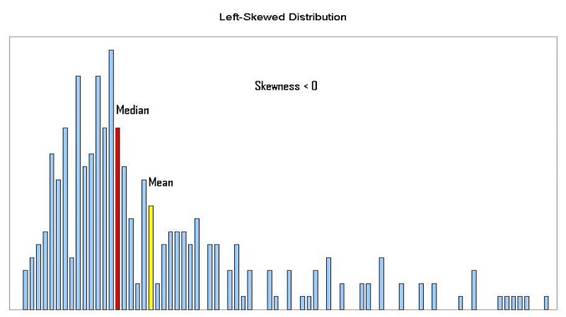
Data sets are sometimes asymmetrical.  For example, for a left-skewed data set, the median will be lower than the mean, and the skewness will be negative, as seen in this chart:


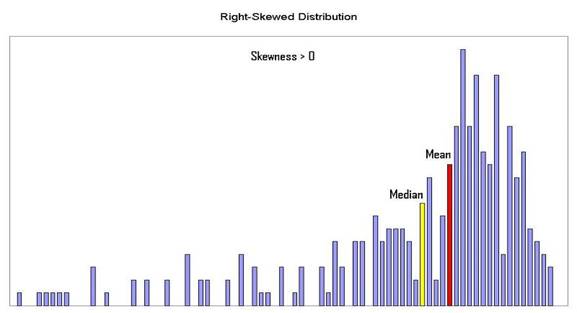
In right-skewed data sets, the median is greater than the mean, and the skewness is positive:


In a high kurtosis distribution (kurtosis > 3), data will be clustered much more about the mean, and the tails will be relatively lighter.  The chart below shows a distribution with a relatively high kurtosis (5.3); this distribution has a high proportion of its data points clustered about the mean, and the tails are very light:


Among the commonly-encountered probability distributions described in statistics, the Bernoulli distribution (for probability close to 0% or 100%), Laplace distribution and the logistic distribution tend to have high kurtosis values.

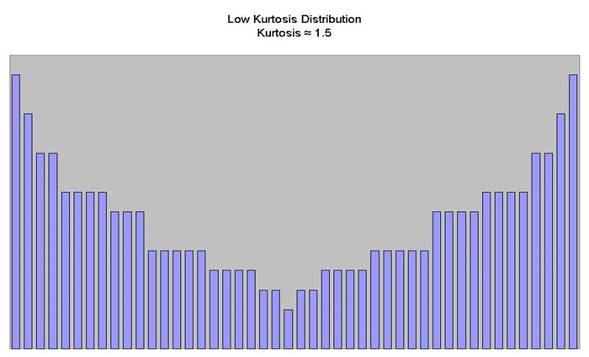
In a low kurtosis distribution (kurtosis < 3), data will not have a pronounced peak about the mean, and will consequently have heavier tails, The chart below shows a distribution with a relatively low kurtosis (1.5); this distribution has relatively few data points clustered about the mean, and the tails are very heavy:


Examples of probability distributions with low kurtosis values include the Bernoulli distribution (for probability close to 50%; p = 50% generates the lowest possible kurtosis value, 1), and the discrete uniform distribution.

The formulas for skewness and kurtosis are as follows:

Examples of Kurtosis:

http://en.wikipedia.org/wiki/Kurtosis

The heaviness of the tails of a distribution affects the behaviour of many statistics. Hence it is useful to have a measure of tail heaviness. One such measure is kurtosis. The population kurtosis is usually defined as

Note:   Some statisticians omit the subtraction of 3.  

Because the deviations are raised to the fourth power, positive and negative deviations make the same contribution, while large deviations are strongly emphasized. Because of the divisor , multiplying each value by a constant has no effect on kurtosis.

Population kurtosis must lie between and , inclusive. If represents population skewness and represents population kurtosis, then

Statistical literature sometimes reports that kurtosis measures the peakedness of a density. However, heavy tails have much more influence on kurtosis than does the shape of the distribution near the mean (Kaplansky 1945; Ali 1974; Johnson, et al. 1980).

Sample skewness and kurtosis are rather unreliable estimators of the corresponding parameters in small samples. They are better estimators when your sample is very large. However, large values of skewness or kurtosis may merit attention even in small samples because such values indicate that statistical methods that are based on normality assumptions may be inappropriate.

References:-

Merrian-Webster

http://www.merriam-webster.com/dictionary/kurtosis

Business Dictionary

http://www.businessdictionary.com/definition/kurtosis.html

Experts Exchange

http://www.experts-exchange.com/articles/2529/Median-Mode-Skewness-and-Kurtosis-in-MS-Access.html